El interés compuesto representa la acumulación de intereses que se han generado en un período determinado por un capital inicial (C_I) o principal a una tasa de interés (r) durante (n) periodos de imposición, de modo que los intereses que se obtienen al final de cada período de inversión no se retiran sino que se revierten o añaden al capital inicial, es decir, se capitalizan.

Cálculo del interés compuesto

Para un período de tiempo determinado, el capital final (C_F) se calcula mediante la fórmula

$\ C_{F1} = C_{I}(1+r)$

Ahora, capitalizando el valor obtenido en un segundo período

$\ C_{F2} = C_{F1}(1+r) = C_{I}(1+r)(1+r) = C_{I}(1+r)^2$

Repitiendo esto para un tercer período

$\ C_{F3} = C_{F2}(1+r) = C_{I}(1+r)^2 \cdot (1+r) = C_{I}(1+r)^3$

y generalizando a n los períodos, se obtiene la fórmula de interés compuesto:

$\ C_F = C_I(1+r)^n$

Donde:

\ C_F

es el capital al final del enésimo período

\ C_I

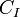es el capital inicial

\ r

es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04)

\ n

es el número de períodos

Para calcular la tasa de interés compuesto total se usa la fórmula:

$\ r_T = (1+r)^n-1$

Donde:

\ r_T

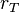es la tasa de interés total expresada en tanto por uno (v.g., 1,85 = 185 %)

\ r

es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04)

\ n

es el número de períodos

Para hacer cálculos continuos en el tiempo en lugar de calcular cantidades para finales de períodos puede usarse la tasa de interés instantánea

\rho

, así el capital final actualizado al tiempo t viene dado por:

$\ C_F(t) = e^{\rho t}$

El resto de tasas pueden calcularse sin problemas a partir de la tasa de interés instantánea.

Obtención de los elementos de la fórmula de interés compuesto

De la ecuación del interés compuesto, para n períodos, se obtiene el capital inicial, conocidos el capital final, el interés y el número de períodos:

\ C_I = \frac{ C_F} {( 1 + r)^n}

El número de períodos puede calcularse, conocidos los capitales inicial y final y el interés, despejando n en la última fórmula, obteniéndose:

\ n = \frac{\log(C_F/C_I)} { \log(1 + r) }

El interés puede calcularse, conocidos los capitales inicial y final y el número de períodos, despojándole de esa misma fórmula:

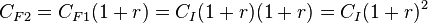
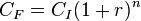
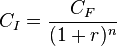
r = \left( {\frac{C_F} {C_I}}\right)^{\frac{1} { n}}- 1= \sqrt[n]{\frac{C_F} {C_I} }- 1