ANUALIDAD
-Cantidad de dinero igual
-En periodos y tiempos iguales
-No tiene que incluir forzosamente en plazo de tiempo anuales
AMORTIZACIÓN
-Es la cantidad de dinero que salda gradualmente una deuda
-Considerando los intereses que genera dicha deuda
-Respetando los plazos de tiempo estipulados
ejemplo:
Institucion
capital: 463200
tasa de interes : 39% anual
tiempo: 5 años
tiempo 30 bimestres
interes: 0.058333333
| ALTERNATIVA 2 | fecha de pago | anualidad | interes | amortizacion | saldos | 0.05833333 | 463200 | |
| 1 | 26/12/2015 | $33,053.06 | $27,020.00 | $6,033.06 | $457,166.94 | |||
| 2 | 26/02/2016 | $33,053.06 | $26,668.07 | $6,384.98 | $450,781.96 | |||
| 3 | 26/04/2016 | $33,053.06 | $26,295.61 | $6,757.44 | $444,024.52 | |||
| 4 | 26/06/2016 | $33,053.06 | $25,901.43 | $7,151.63 | $436,872.89 | |||
| 5 | 26/08/2016 | $33,053.06 | $25,484.25 | $7,568.80 | $429,304.09 | |||
| 6 | 26/10/2016 | $33,053.06 | $25,042.74 | $8,010.32 | $421,293.77 | |||
| 7 | 26/12/2016 | $33,053.06 | $24,575.47 | $8,477.59 | $412,816.18 | |||
| 8 | 26/02/2017 | $33,053.06 | $24,080.94 | $8,972.11 | $403,844.07 | |||
| 9 | 26/04/2017 | $33,053.06 | $23,557.57 | $9,495.49 | $394,348.58 | |||
| 10 | 26/06/2017 | $33,053.06 | $23,003.67 | $10,049.39 | $384,299.19 | |||
| 11 | 26/08/2017 | $33,053.06 | $22,417.45 | $10,635.60 | $373,663.59 | |||
| 12 | 26/10/2017 | $33,053.06 | $21,797.04 | $11,256.01 | $362,407.58 | |||
| 13 | 26/12/2017 | $33,053.06 | $21,140.44 | $11,912.61 | $350,494.96 | |||
| 14 | 26/02/2018 | $33,053.06 | $20,445.54 | $12,607.52 | $337,887.45 | |||
| 15 | 26/04/2018 | $33,053.06 | $19,710.10 | $13,342.96 | $324,544.49 | |||
| 16 | 26/06/2018 | $33,053.06 | $18,931.76 | $14,121.29 | $310,423.20 | |||
| 17 | 26/08/2018 | $33,053.06 | $18,108.02 | $14,945.04 | $295,478.16 | |||
| 18 | 26/10/2018 | $33,053.06 | $17,236.23 | $15,816.83 | $279,661.33 | |||
| 19 | 26/12/2018 | $33,053.06 | $16,313.58 | $16,739.48 | $262,921.85 | |||
| 20 | 26/02/2019 | $33,053.06 | $15,337.11 | $17,715.95 | $245,205.90 | |||
| 21 | 26/04/2019 | $33,053.06 | $14,303.68 | $18,749.38 | $226,456.52 | |||
| 22 | 26/06/2019 | $33,053.06 | $13,209.96 | $19,843.09 | $206,613.43 | |||
| 23 | 26/08/2019 | $33,053.06 | $12,052.45 | $21,000.61 | $185,612.82 | |||
| 24 | 26/10/2019 | $33,053.06 | $10,827.41 | $22,225.64 | $163,387.18 | |||
| 25 | 26/12/2019 | $33,053.06 | $9,530.92 | $23,522.14 | $139,865.05 | |||
| 26 | 26/02/2020 | $33,053.06 | $8,158.79 | $24,894.26 | $114,970.78 | |||
| 27 | 26/04/2020 | $33,053.06 | $6,706.63 | $26,346.43 | $88,624.36 | |||
| 28 | 26/06/2020 | $33,053.06 | $5,169.75 | $27,883.30 | $60,741.05 | |||
| 29 | 26/08/2020 | $33,053.06 | $3,543.23 | $29,509.83 | $31,231.23 | |||
| 30 | 26/10/2020 | $33,053.06 | $1,821.82 | $31,231.23 | - 0.01 |

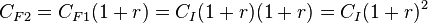

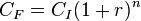
 es el capital al final del enésimo período
es el capital al final del enésimo período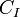 es el capital inicial
es el capital inicial es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04)
es la tasa de interés expresada en tanto por uno (v.g., 4 % = 0,04) es el número de períodos
es el número de períodos
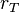 es la tasa de interés total expresada en tanto por uno (v.g., 1,85 = 185 %)
es la tasa de interés total expresada en tanto por uno (v.g., 1,85 = 185 %) , así el capital final actualizado al tiempo t viene dado por:
, así el capital final actualizado al tiempo t viene dado por:
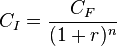

![r = \left( {\frac{C_F} {C_I}}\right)^{\frac{1} { n}}- 1= \sqrt[n]{\frac{C_F} {C_I} }- 1](https://upload.wikimedia.org/math/5/e/1/5e18417e6346aac505bcaf963c050be1.png)
